Geometry: Non-Central Angles, Interior and Exterior Angles, and Secant and Tangent Relationships of Circles

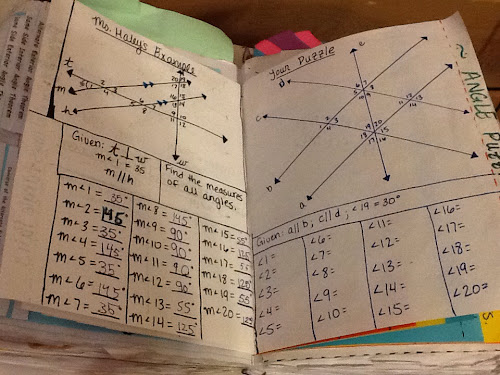
Pg 5. Non-Central Angles (Need to rethink the title now that I think about it.)

This page consists of a half page fold of two pages glued together with four half page folds on each page. This entire page is pulled from the CSCOPE curriculum and tweaked just a bit.

First, we completed a page/lesson using paper folding and making conclusion based on what we know. When complete, the students would make a conclusion based on the evidence. We wrote that on the front off that page. After we completed all four pages, we went to the front and wrote three summarizing conclusions. I think it went pretty well and soundly build and understanding.

First section:

Left side:

I drew up a general diagram for the following three pages. We then completed the lesson with the same diagrams.

Right side:

Second Section:

Left side:

Right side:

 

Pg 6. Circles, Lines, and Angles

I want to find a better way to present and organize the following two pages. My students understood, but it didn't make a lasting impact.

 

 

 

Pg 7. Secant and Tangent Relationships

 

 

 

Posted with Blogsy

Geometry: Triangle Congruency and Similar Triangles

Pg 13. Congruency and Similarity Relationships

This is a half page book fold with half page extensions on the inside.

We first wrote and diagramed all triangle congruence theorems.

We then briefed over similar and non congruent.

Finished with CPCTC and two proofs.

 

 

Pg 14. Proof Patterns of Congruent Triangle Proofs

The first year I taught, I noticed that students struggled with proofs. My third year, I decided to focus on building a pattern/strategy for proving congruent triangles.

1. Label what is given.
2. List the triangle congruency theorems/postulates we could use.

3. Start with the given.

4. Prove by listing the needed information (side, then angle, then side). This began to vary as the diagrams and proofs changed.

5. Prove statement.

 

Pg 15. Proof Book

This was a collection of about eight proofs. The students would complete one to two proofs each day as warmups. Any down time we had, the proof book would be used.

 

Pg 16. What Makes Triangles Congruent

This was originally a warm up quiz that turned into an impromptu lesson and journal page. As I graded their completion immediately, I noticed that many students struggled with number eight.

IMPROMPTU LESSON: I grabbed some patty paper (awesome stuff) and we traced the two triangles from the given statement and labeled the congruent segments. Once the triangles were separated, students saw the relationships and congruency.

We folded the paper in half (my go to impromptu journal fold) and glued the patty paper to the front.

Pg 17. Similar Triangles

 

Pg 18. Similar Postulates, Theorems, and Proofs

This was a new area for me this year so it's going to be a little rusty.

The statements on the front are actually students conclusions based on our warmup discussion while prepping (passing out papers, getting journals, etc.).

 

 

Posted with Blogsy

Geometry: Applying Parallel Lines, Transversals, and Special Angle Pairs with a Mini Flip Book

Pg 4. Over the past three years, I have approached these theorems/postulates in different ways.

First attempt: Completed a worksheet and summarized our findings as seen below.

Second attempt:

We completed two flip books with sentence strips that the students had to match the if statement to the then statement and to the diagram.

Third attempt:

Within a large flip book project, we wrote the postulates/theorems out along with each converse.

For the large flip book project, students were to google an image that they could illustrate parallel lines and a transversal on.

INTERESTING: Students brought up the interesting difference between parallel in the real world versus the result of a two dimensional image. For example, one student wanted to use an image of railroad tracks knowing that they were parallel in the real world. However, another student pointed out that when viewed on a two dimensional service the tracks appeared to intersect at the perspective point. Is the picture a valid option? After this discussion, I had students justify their chosen image. How did the idea of parallel apply?

Next, they labeled the angles and identified the special angle relationships.

This had some interesting results. I had the students make up some algebra problems, solve and check them, and then exchange with a partner. Some of the results the students would makeup would have infinite solutions, no solution, and result in negative angle measures.

Here are the postulates/theorems and converses.

 

 

 

 

Out of all that I teach in Geometry, this is one of the hardest concepts to get my students to understand. Proving lines paralell or angles congruent. It took me two years to see the pattern. Maybe next year I will be able to present it better.

 

I gave students two angle puzzles to complete. We discussed every detail and justified each strategy used. Next, students were to create their own angle puzzles for homework. The next day, I mixed up each puzzle and passed them out to the class. Great idea, but kind of overwhelming. Students could critique and troubleshoot each others puzzles, but some would use incorrect properties and their answers wouldn't work out. This activity requires quite a bit of time and would probably do better if the students work with a partner.

 

Posted with Blogsy

Geometry: Angle Relationships

Pg 15. Angle Addition Postulate

The bottom half is a manipulative used to physically demonstrate the Angle Addition Postulate. The yellow rectangle was glued down 'like a pocket' for angles 1 and 2.

Pg 16. Angle Relationships

 

 

I use the layered flip book quite a bit.

 

Posted with Blogsy