I have found that even after defining these two properties, students do not really recall or understand them. I added these four practice problems and focus the guiding questions on which method would be easiest or most appealing for mental math.
After we worked through the above problems, students were able to identify the properties when asked and even identified them when they were applied later on.
Some colleagues and students have requested typed notes. I have been slowly working on typing old notes. This is not my go-to strategy. I'm very hands-on and pen to paper.
My journal notes strategy or folding method is simple once you figure out my pattern.
They will not print perfectly or fold exactly!
Most all notes are folded in half (half page folds are what I call them). And I'm very proportionate as far as dividing things in half, fourths, sixths, eighths, etc.
Printing: The first two pages of notes (not including attached notes/foldables by glue) are to be printed two sided. I change the print setting on my computer to two sided flip on short edge. A colleague of mine, prints them one sided and then figures out the two sided at the copier. Each additional page to be attached is printed one sided. Some people claim it as a waste; however, I have a ton of scratch paper with one blank side that I run through the copier for these notes.
Attached notes/foldables that are glued to the half page notes are usually a two sided print.
So far, I have only figured out how to upload PDF documents to google drive. Word documents when uploaded mess up the tables, images, etc. If you would like a copy of one of the documents for Microsoft Office Word, email me at journalwizard@gmail.com . To access the uploaded PDF documents, I believe you have to have a google account. If anyone knows how to put these documents directly into my blog, LET ME KNOW!
To get a copy of any notes click PDF Documents at the top of the blog and you'll be sent to google drive where hopefully the notes are available.
These notes reference and use information pulled directly from Glencoe Course 3, Holt PreAlgebra, and Holt Algebra 1 textbooks. (I'm also located in Texas, I don't know how different our "TEKS" and 'stuff' is from other states and countries.)
My journal pages are now working towards a compilation of foldables within a larger foldable. I try to devote a page to a concept with a combination of approaches-definition, strategies, manipulatives, etc.
For Algebra, I wanted to review to coordinate plane. I used a half page overall and divided into sections. One section was for definitions.
The second was for the foldable that diagramed the components.
Students liked this page because we stepped outside my traditional boring half page book.
Pg 5. Non-Central Angles (Need to rethink the title now that I think about it.)
This page consists of a half page fold of two pages glued together with four half page folds on each page. This entire page is pulled from the CSCOPE curriculum and tweaked just a bit.
First, we completed a page/lesson using paper folding and making conclusion based on what we know. When complete, the students would make a conclusion based on the evidence. We wrote that on the front off that page. After we completed all four pages, we went to the front and wrote three summarizing conclusions. I think it went pretty well and soundly build and understanding.
First section:
Left side:
I drew up a general diagram for the following three pages. We then completed the lesson with the same diagrams.
Right side:
Second Section:
Left side:
Right side:
Pg 6. Circles, Lines, and Angles
I want to find a better way to present and organize the following two pages. My students understood, but it didn't make a lasting impact.
Pg 7. Secant and Tangent Relationships
These are my resources from an iPad training.
Resources:
Pending: (Apps I have not used, but shared by other teachers.)
Resource:
Apple TV: Used to project your iPad activities.
I have struggled with this unit for the past three years. I do a great job with the geometry side, but the algebra is really tough to handle. I'm not sure what skills my students have coming in from Algebra 1 and in my first two years I ended up bogged down reteaching. My third year, I set a schedule and limited myself to a set number of days and pushed through. I made my primary focus applying geometry on the grid and tried to make the algebra as logical and visual as possible.
These journal pages are from my second year of teaching.
Pg 1. Unit 2 Coordinate Geometry
My first attempt at teaching slope with a foldable.
Pg 3. Slope - Intercept Form
I now like to pair rise over run with fall over crawl.
Pg 4. Parallel vs. Perpendicular
Pg 4. Over the past three years, I have approached these theorems/postulates in different ways.
First attempt: Completed a worksheet and summarized our findings as seen below.
Second attempt:
We completed two flip books with sentence strips that the students had to match the if statement to the then statement and to the diagram.
Third attempt:
Within a large flip book project, we wrote the postulates/theorems out along with each converse.
For the large flip book project, students were to google an image that they could illustrate parallel lines and a transversal on.
INTERESTING: Students brought up the interesting difference between parallel in the real world versus the result of a two dimensional image. For example, one student wanted to use an image of railroad tracks knowing that they were parallel in the real world. However, another student pointed out that when viewed on a two dimensional service the tracks appeared to intersect at the perspective point. Is the picture a valid option? After this discussion, I had students justify their chosen image. How did the idea of parallel apply?
This had some interesting results. I had the students make up some algebra problems, solve and check them, and then exchange with a partner. Some of the results the students would makeup would have infinite solutions, no solution, and result in negative angle measures.
Here are the postulates/theorems and converses.
Out of all that I teach in Geometry, this is one of the hardest concepts to get my students to understand. Proving lines paralell or angles congruent. It took me two years to see the pattern. Maybe next year I will be able to present it better.
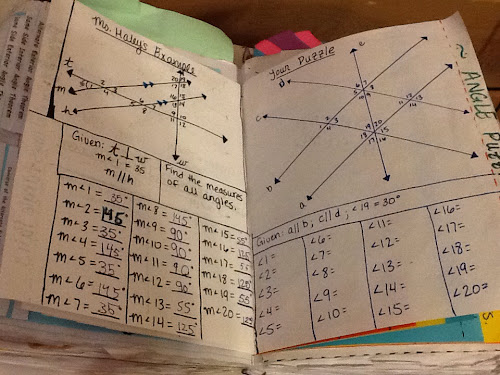
I gave students two angle puzzles to complete. We discussed every detail and justified each strategy used. Next, students were to create their own angle puzzles for homework. The next day, I mixed up each puzzle and passed them out to the class. Great idea, but kind of overwhelming. Students could critique and troubleshoot each others puzzles, but some would use incorrect properties and their answers wouldn't work out. This activity requires quite a bit of time and would probably do better if the students work with a partner.
Posted with Blogsy